歪み（＝ウェーブシェイプ）って、ある意味、極論を言えば味気ないんですよね。。
なぜってちょっと深く歪めただけで、大体似たような質感に変わってしまうわけですし、 音の傾向も何れもザラザラして、ノイジーな傾向にあって、それがどれだけの量かっていうパラメータしかない感じです。 何しろ歪みは第四回でも触れましたとおり、「ある音量を別の音量で置き換えるという処理」でしかありません。 時間方向の情報は基本的には何も使わないのです。音は時刻と振幅の２次元の情報 （本当をいうと１サンプル当たり1次元と考えて無限に近い次元と考えるのが数学人のスジらしいのですが、、）なのに、 1次元の操作しかしていないわけです。
そんな分けで昔から歪みを彩るために色々な工夫が行われてきました。

まず第一に考えられるのは、歪みは歪みで置いて置くとして、歪みの前後にフィルタをかけるというやり方です。
これはギターアンプやギター用の歪み系エフェクタなんかで、トーンコントロールと呼ばれているツマミ類に相当します。 歪み回路を通す前後で、低音（BASS)、中音（MIDDLE)、高音（HIGH）、あるいは超高音（PRESENSE)のカット／ブースト量を 調整することで、歪み単独では無理だった独特の質感を得ることができます。
よくやるのが、歪み前のフィルタで、MIDDLEをカットしてドンシャリにしておいて、歪みの後でMIDDLEをブーストする、 みたいに前後で相殺し合うようなフィルタの設定を使って、歪みの帯域毎のクセを強調するといった設定です。

また実のところ、ギターアンプのキャビネット（スピーカー）自体がフィルタとしての性質を持っていて、 アンプシミュレータなんかだと、歪み回路とキャビネットを独立して選択できるようになった製品が多いかと思われます。

でも、こういう彩り方って、既にオーソドックスというのか、広い意味ではもう飽きたので、今回は別の彩り方を紹介します。。。。

隠し味は波形で行こう

味付けをするには、やはり別の波形をミックスするのが基本です、 かっこよく言えばベクターシンセシスだったりしますし、平たく言えば複数の波形のミックスです。 非常に単純ならが音声合成の方法としては最も基本且つ、自然な効果が得られます。

歪める対象の波形に何か別の波形をミックスして、それを歪める

さて今度は今の話に別の波形を混ぜて見ましょう。
Ｘ＝Ｂ＋Ａと、Ｙ＝Ｂ−Ａを考えます。 当然ＸとＹを何も歪めずにミックスすると、Ｘ＋Ｙ＝（Ｂ＋Ａ）＋（Ｂ−Ａ）＝２×Ｂなので、Ａは相殺して消えます。
ところがＸとＹを各々Ｄに通した後にミックスする場合は、Ｄ｛Ｘ｝＋Ｄ｛Ｙ｝＝Ｄ｛Ｂ＋Ａ｝＋Ｄ｛Ｂ−Ａ｝となりますが、 Ｄはいわゆる非線形エフェクトというやつで、足し算引き算や掛け算の関係をＤの外側に持ち出すことができません。
なので、これ以上は式を簡略化できません。つまりＤ｛Ｘ｝＋Ｄ｛Ｙ｝にはＡの影響が残るわけです。
しかしＤが音楽で使われる普通のディストーションだと仮定すると （笑、もうちょとそれらしく言うと少なくとも(０≦|Δａ|＜小さな定数μ)の時、入力波形の２つのレベルａとａ＋Δａに対して、|Δａ|が小さくなるに従って |Ｄ｛ａ｝−Ｄ｛ａ＋Δａ｝|も小さくなると仮定すると） Ｄ｛Ｘ｝＋Ｄ｛Ｙ｝の振幅は、Ｂの振幅に従って増減するといえるものと思われます。
おまけに線形性が高い区間では、Ｄ｛Ｘ｝＋Ｄ｛Ｙ｝≒ｃ×（Ｘ＋Ｙ）≒ｃ×２×Ｂ（ｃは適当な定数） となります。

平たく言うと、隠し味Ａはそれなりの影響を及ぼしながらも、おおむね相殺されるわけです。 特にメインの音Ｂが小さな音量の場合は、より相殺されて無音に近づきます。 (更に言うと僕の書いた数式はマガイモノですのでご注意下さい。)

なおディストーションを実現するアルゴリズムは、最大振幅が決まっていることが普通なので、 ディストーションに入力する前に同一増幅率のアッテネータなり、コンプレッサをかけておくと良いです。

以上の話を図にするとこうなります。

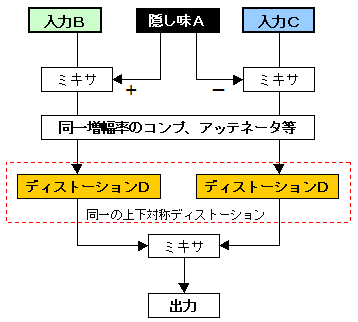
ダイアグラムみたいになっていて、一見すると特化したソフトなりハードが必要と思われるかも知れませんが、 要は位相を反転した音をそれぞれの入力波形にミックスした後、各々同じディストーションをかけて、 その結果をミックスするだけなので、波形編集ソフトの操作でも頑張ればできるかと思われますし、僕自身も頑張りました。

例えばこんな隠し味。。。

以降は入力波形Ｂ，Ｃと隠し味Ａの組み合わせについて、ボクが試した結果と考察を書いてみようかと思います。 なお、以下の音声サンプルは全て192KHzのサンプリング周波数で処理したのち、44.1KHｚにダウンサンプリングしたものです。

♪Ｂ＝Ｃ＝素の入力波形、Ａ＝サイン波

聞いてみる
隠し味にサイン波を用いると、何てゆーか、昔のサンプラーというのか、サンプリング周波数が低くて補間処理もやっていないような、 ローファイ感漂う出力音になります。
実際にサンプリング周波数をリアルタイムで滑らかに変更するってのは以外と難しいものなので、それっぽい質感を演出したい場合は、 このやり方は重宝するのではないかと思います。

♪Ｂ＝Ｃ＝素の入力波形、Ａ＝ホワイトノイズ

聞いてみる
歪んでいるところだけにノイズがのった感じになります。荒れた音って感じです。いやディストーションなので、荒れていて然るべきなのですが、、 またちょっと趣きを異にしたアレです。ミックスする音量を調整したり、ハイパスフィルタを通すなどして、もう少し控えめというか、 うっすらとノイズが載る、シルキーな感じを表現することも可能かと思われます。
あるいは、ローパスフィルタで超低音だけを通して、これを大きめにミックスすることで、 「あまり歪んでいないようだけど、何故かボコボコ」といった質感を表現できよう。

♪Ｂ＝Ｃ＝素の入力波形、Ａ＝素の入力波形にフランジをかけた音

聞いてみる１
実はディストーションとフランジ（あるいはコーラス）は、相性がいいエフェクトです。
知らない人のために教えちゃうと、ディストーション→コーラスではなくて コーラス→ディストーションと繋ぐことによって非常に過激な歪み感を作り出すことができます。
これは、いわゆるコムフィルタという効果によって、フィルタとして特性が劇的に変わることや、 ディレイによって音がダブって聴こえるなどの、相乗効果によるものと思われます。
その反面、これらのエフェクトはビブラート効果によって、ピッチ感が曖昧になってしまうという副作用がありました。

しかし、今回のテクニックを使えば、ビブラートの掛かった成分自体は相殺されて、 振幅の落差として現れてくる部分のみ（正確には何と言えばいいのか分かりません、、）が残されることにより、 過激さを維持しつつ、ピッチの正確さを維持することができます。
このパターンが今回実験した中では、一番オススメだったので、サンプルサウンドをもう1個どうぞ。

聞いてみる２　 (前半が普通のディストーション、後半がフランジ成分を隠したディストーションです)

♪Ｂ＝Ｃ＝素の入力波形、Ａ＝素の入力波形にディストーションをかけた音

聞いてみる
いわゆるファズ系のサウンドになります。ディストーションＤで歪んでいる時のみ、Ａの歪み成分が現れる、 しかも歪みに歪みを加えて極端な歪みになるわけです。
Ａにディレイをかけることで、更にニュアンスをコントロールできるものと思われます。

♪その他、色々

アイデア次第でいろんなパターンが作れるかと思います。
Ｂ＝素の入力波形、Ｃ＝素の入力波形にリバーブ、Ａ＝素の入力波形にハイパスフィルタ
Ｂ＝素の入力波形、Ｃ＝素の入力波形にコーラス、Ａ＝ノイズ
Ｂ＝Ｃ＝ミニマムなシーケンスサウンド、Ａ＝クラシック音楽
などなど、、さらにＡを完全には相殺しないという発想もあるかと思います。
Ｘ＝（Ｂ＋Ａ）と、Ｙ＝（Ｂ−Ａ×適当なゲイン）とやって、 微妙にＡが漏れたり漏れなかったりをコントロールしたりもできると思います。