(2005.08.16)
つい先日まで、「また新たな発明を思い付いた!」「今度のは凄いぞ!またまた特許出願じゃ!!」
と意気揚々と息を弾ませながら試作のプログラムをカリカリと書いておりました。
それはもう得意気というか幸せ一杯な気分だったのですが、、、、
もう10年も前に先を越されていました。(TT*そのアイデアというのは、周波数・時間分析でよく使われているガボールフィルタの高速化に関するものでした。
→此処にある罠
(リンク先でPDFのリンクをクリックしてみてください。)
まあ、やろうとしている事が(技術の分野としては)超メジャーな分野ですし、信号処理や確率論の入門書の最初の方のページに書かれているようなアイデアの組み合わせだったので、 誰が思い付いていても不思議ではなかったのですけどね、、、
僕がしばらくの間(約3ヶ月もの間)、先を越されていたのに気が付かなかったのは、「ガボール」とか「高速」とか、「畳み込み」とかで 適当に組み合わせて検索をかけてもそれらしいものが見つからなかったからです。念のため"gabor"とか"fast"とかで検索をかけてみたら、、、
「あんじゃん、、」という分けでした。〇rz
しかし、そんなこんなで落ち込んでいても仕方がないし、せっかく自分の頭も捻って考えたものには違いがないわけで、 せめて知識のひけらかしでもして憂さを晴らすこと位のことはできるだろうと思い、ここにそのテクニックを紹介させて頂きます。。m(_ _)m
矩形窓
矩形窓ってありますよね。要するに単純な重みを付けない移動平均値を求める操作といか、
音声信号や、株価みたいな連続するデータに対して、ある一定区間の平均値を区間をちょっとずつずらしながら
求めていくというあれです。
矩形窓以外は重み付き移動平均となっていて、それぞれ重みを付けるグラフの形状によってハミング窓とかハニング窓とかブラックマン窓とか、そしてガウス窓など色々あります。これらは総称して窓関数といいます。
窓関数の目的は、1つには細かい変動をフィルタリングして、大まかな傾向を掴むために使うというものです。
このため窓関数と言われているグラフをインパルス応答の波形として捕らえた場合(実のところ広義の移動平均法=FIRフィルタ=畳み込みなのです)、
その周波数特性は0Hzにピークを持つローパスフィルタとなっています。
この目的からすると基本的には高い周波数の成分が少ない方が良いフィルタということになります。
もう1つはフーリエ変換みたいに無限に続く区間全体を対象にしないと正しい結果が得られない変換処理で、
それでも短い範囲を切り出して分析などを行いたい場合、切り出した波形の前後がブツ切れになって、
特に高い周波数帯がかき乱されないようにすることです。
これは図にすると直ぐに分かるかと思います。
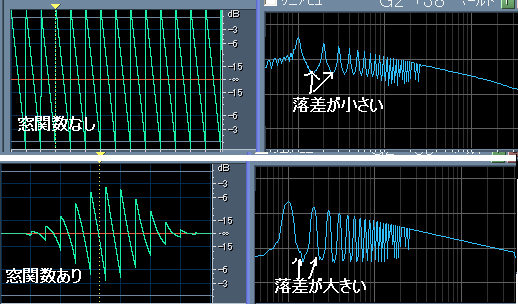
上側の画像が窓関数を施していない(実を言えば矩形窓を施している)100Hzのノコギリ波と、そのFFT表示です。
下側の窓関数を施したものは、上側と比べて周波数特性の山と谷の落差が大きい、
つまりは周波数特性がはっきりしたものになっているということが分かります。
窓関数によって、切り出す波形の前後をフェーディングすれば、幾分かは正確な周波数特性を計ることができるというわけです。
ただしフェーディングという処置事態が、窓関数と対象の波形とのAM変調(和と差の周波数になっちゃう、更に一般化して言うと時間領域での掛け算は周波数領域での畳み込みになっちゃう)になりますので、やはり窓関数自体の倍音(?)が少ない方が正確な結果が得られます。(10Hzか20Hz程度の誤差なら許せるけど100Hzは痛い、そんな感じ)
矩形窓はいわゆる窓関数の中では最も単純なものです。
「連続する信号やグラフから一定区間を切り出して、集計やら変換処理を行う」ということをやった時点で実は勝手にかかっているのが矩形窓で、
アルゴリズム上、特別なことは何もやっていないのです。
矩形窓は計算量も実に少ないです。一定区間の重み無しの移動平均値(矩形窓の別の呼び方ですね)を求めるには、集計区間を移動する毎に(1サンプル読む毎に)区間の先頭として現在のサンプル値を足しこみ、区間の末尾の値を差し引く(次の区間に移動するわけだから末尾の値は消えます)ということをやって、その結果を区間数で割ればよいのです。
実に足し算1回、引き算1回、割り算1回です。(実際には最初に逆数を計算しておくので、ループ内の割り算は掛け算で代用できます。)
他の窓関数では重みの再計算が必要となりますので、1サンプル毎に区間数分の積和演算が必要となってしまいます。
最後に、矩形窓のグラフ(インパルス応答)と、周波数特性をご覧に入れましょう。
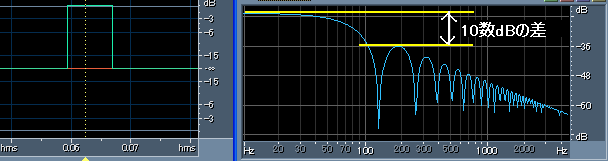
どうでしょうか?、矩形窓も窓関数の「おきて」に従って0Hzに最初の山があります。しかし120Hz付近に現れてくる2つ目の山は0Hzの山と比べて、
高々10数dB程度の差しかありません。より高い周波数の方を見ても減り方は実になだらかです。
これが矩形窓の最大の弱点で、簡単に計算できる割に、窓関数としては以外に不人気なゆえんです。
ガウス窓
ガウス窓というのは、インパルス応答が正規分布となる窓関数です。
正規分布(釣鐘型曲線)というのは、確率統計の入門書の最初の方のページに出てくるアレです。左右対称の形をしていて、山と裾を持っている波形です。
フィルタとして見た場合の最大の特徴は、先ほど矩形窓の問題として挙げていました周波数特性の2つ目以降の山がとても小さい(無い@数学)ということです。
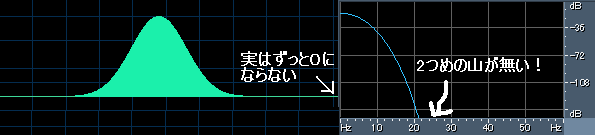
そして、最大の問題は、インパルス応答が非常に長い(じつは無限長)ということです。インパルス応答の主要な部分(山)は割と短い時間幅しかありませんが、裾の部分が小さな値ながらもずっと0にはならずに広がっているからです。この裾の部分はもちろんあるレベルで0になったものとしてカットしてしまうこともできるのですが、やはりそれなりに誤差が発生しますのである程度の裾の長さは必要です。なので正確にやるには、中央の主要な成分と比べて殆んど0に見える小さな振幅の部分をなるべく余裕をもって長く処理する必要があるため、まともに計算すると効率が悪いですし、フィルタとして考えるとレイテンシ(出力信号全体の遅れ)が大きくなってしまう問題もあります。(要するにアタックが遅い波形だから)
そうはいってもガウス窓には他にも色々と便利な性質(たとえばガウス窓同士を畳み込むと幅は変われど形が変わらないとか)があるため、人気の高い窓関数なのです。
ガボールフィルタ
ガボールフィルタというのは、入力信号の中に「どの時点で、どの周波数帯の成分が、どのくらい含まれているか」
を調べるために使われるフィルタです。1つのガボールフィルタには中心周波数というのが1つあって、
この中心周波数を中心にして左右対称になだらかに減衰するような周波数特性を持っているフィルタです。
どのようなインパルス応答の波形になるかといいますと、ガウス窓とサイン波を掛け合わせた(AM変調した)波形と、
更にガウス窓とコサイン波(位相が90度ずれた波形)を掛け合わせた波形を、ペアで使います。(つまりサイン波のものと、コサイン波のもの
、それぞれをインパルス応答として持つフィルタのペアです。)
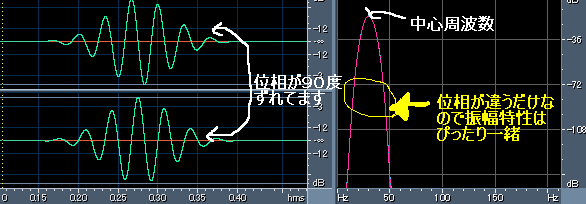
2つのフィルタの「2-ノルム」(それぞれのフィルタの出力を自乗した値同士を足し合わせた結果の平方根)を求めることで、入力信号が持つその周波数帯域でのエンベロープを得ることができます。
まるでAMラジオのチューナーみたいなフィルタなのです。
より正確な周波数の分布を知りたい場合は、波長に対して窓のサイズを大きくとります。
この場合エンベローブの正確さ(エンベローブ自体が含み得る高調波成分)は抑えられてしまいます。
逆にエンベローブをなるべく細かく計りたい場合、波長に対して窓のサイズを小さくとりますが、
これまた逆に周波数の分布が不鮮明になります。
この2つ(周波数とエンベローブ)を同時に正確に計ることはできないとされていますが、
ガウス窓はその両者のトレードオフを最も無理ムラ無駄なく調整できることが知られているようです。
ここまで足早に説明してきましたが、ここからようやく僕が思いついたと勘違いしていたアイデアの説明をさせて頂きます。
矩形窓×矩形窓×・・・≒ガウス窓
僕ははっきり言って数学オンチなので、詳しい数式やら証明やらはできないのですが、しかし一般に言われている数学的知識を使って、 自分(だと思っていた)のアイデアを説明することくらいはできます。
さて、僕はここのところ確率論の勉強をしています。なので、窓関数を確率分布になぞらえてみますと、矩形窓は一様分布という
ことになります。
で、特定の分布を持つ独立な確率変数の和の分布は、元の分布の畳み込みで表されることが知られています。
ちなみに3つの独立な確率変数の和の分布は、元の確率分布を3回畳み込んだ結果となります。
では、無数の独立な確率変数の和の分布はどうなるかというと、少なくとも一様分布だったら(そうじゃなくても大抵は)正規分布に収束することが知られています。(中心極限定理)カコイイヨネ
それも5、6個くらいでもかなり正規分布っぽくなります。
今の僕の能力ではこれ以上踏み込んだ説明はできませんので、これにて証明終わりとさせて下さい。
窓関数の話に戻って考えますと、矩形窓同士で何回も畳み込むとガウス窓に近づくと言えます。
ちなみに中心極限定理を最初に証明したのがガウスという人なのです。
で、これは僕しか知らないと思っていたのは、兎の中の蛙もいいところで、最初に挙げたEPFL The biomedical imaging groupでは、
これをBスプライン窓(B-Spline Window)として紹介しています。(そんなもんだったっけ?)
Bスプライン窓の特徴は、正規分布に似た形をしていることの他に、インパルス応答が有限長(compactly supported)、そしてなんといっても計算量が少なく、窓サイズ(インパルス応答長)に影響されないことです。
My試作品
ガボールフィルタの高速化に関して、2つのアイデアを投入しました。1つは今説明したBスプライン窓を使うことです。
そしてもう一つは、窓関数をかける前に入力信号に対してサイン波やコサイン波との乗算をやっておくということです。
つまり入力信号を「サイン(コサイン)波とガウス窓を掛け合わせた信号により畳み込む」のではなく、「入力信号にサイン(コサイン)波を掛け合わせた後の信号を、ガウス窓により畳み込む」
とした訳です。
普通はフィルタを考える場合、インパルス応答は固定とするのが正しいやり方でしょう。
「インパルス応答」として考えた場合、僕のやり方だと1サンプル毎に、サイン波の部分が回転していくような変なフィルタとなってしまいます。
しかし、1つのサンプルに特定して考えると、それまでのサンプルを「サイン(コサイン)波とガウス窓を掛け合わせた信号により畳み込んだ結果」というのに変わりは無く、
また、サイン波とコサイン波の2−ノルムはどの時点でも一定で、さらに調べたい物が正にそのノルムの変化によって表される波形(つまりはエンベローブ)な
わけなので、1サンプルごとにフィルタのインパルス応答がコロコロと変わったとしても、この場合はさして問題ないかと思った次第です。
また位相に関しても、窓長に対して波長が十分短ければ(窓の中に何周期分ものサイン波が納まっていれば)、サイン波やコサイン波は対称な波形の繰り返しなので、
フィルタリング結果の位相から、現在の位相を引き算すれば(これとは別にレイテンシの調整をさらに後段でやります)、それなりの値になるのではないかと思った次第です。
次に考えましたのは、偽ガウス窓を作るにあたり、矩形窓を何回畳み込みすればいいのか?という問題でした。
ガウス窓らしさを評価する指標を何にするのかという問題ですが、僕はガウス窓をフィルタとしてみた場合に2つめの山が小さいという特徴を、
どれだけ出せているのか?という視点で考えることにしました。矩形窓の2つ目の山は0Hzの山に比べて−10〜−15dB程度ですので、
満足できるレベルを−60dBとすると、大体4〜6回程度の畳み込みを繰り返せば良いかと思いました。
また、矩形窓の長さは整数単位でしかできませんが、これを複数組み合わせた時に結果として作られる擬似ガウス窓の長さが段数の整数倍じゃなければならないとか、
そういう制約を設けたくなかったので、各段の矩形窓の長さを微調整できるようにしました。
具体的にはサンプル数Aの波形と、サンプル数Bの波形を畳み込んだ場合、結果は(A+B−1)のサンプル数となるため、
擬似ガウス窓の長さが100サンプルで、段数が5段の場合、各矩形窓の長さの合計は(104=100+5−1)となります。
これを5分割するために各窓長を21、21、21、21、20というように割り振ることにしました。
それと通常のガボールフィルタでは、窓長と波長の比は、分散を表すσという値で調整するのですが、 それをエミュるだけのノウハウが無かったため、単純にガウス窓の長さに対して、サイン波(コサイン波)が何波長分収まるかというパラメータを使うことにしました。
結果
ソースコード
こちらからダウンロードできます。 基本的な処理は入力ファイルを1chの32Bit浮動小数点値のPCM生データとして取り込んで、複数(GABOR_CNT個)のガボールフィルタで処理し、 それぞれの出力結果を、1、2、1、2、・・・形式の2chの32Bit浮動小数点値のPCM生データで保存します。1chに振幅、2chに位相を書き出しています。ファイルを書き込む際にレイテンシを処理している部分が少々泥縄となっておりますが、ご容赦下さい。
また、ディスク容量やら限界値のテストなどはしておりませんので、あしからず。。。
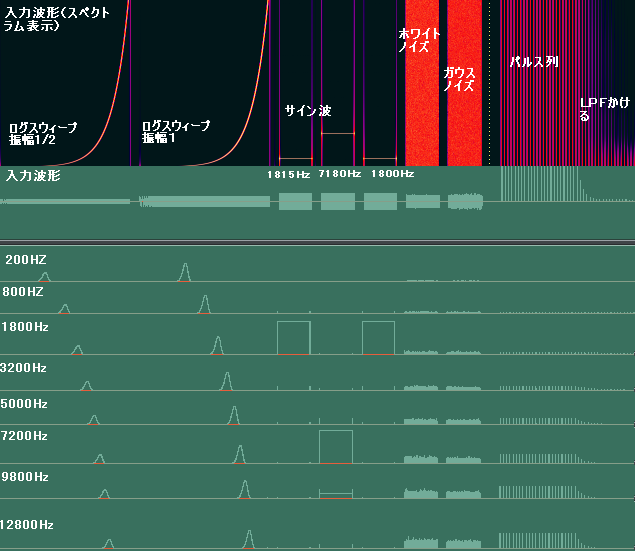
動作結果の図
コメントは図中に書きましたので省略されて頂きます。